Background
The obvious reason for the existence of interactive theorem proving (ITP) is that automated theorem proving only works for problems of limited difficulty and size. ITP has been successfully applied to many problems that are out of the scope of current automated theorem proving technology and will stay so for a long time to come. Maybe the three most notable of these applications are the proof of the four colour theorem in Coq, the verification of the seL4 microkernel in Isabelle, and most recently the proof of the Feit-Thompson odd order theorem in Coq. Of major interest is also the ongoing mechanisation of the proof of the Kepler conjecture in HOL Light and Isabelle through the Flyspeck project.
| Duration | Number of people | Lines of verification code | |
|---|---|---|---|
| Four colour theorem | 2000-2005 | 1 | 60000 |
| seL4 microkernel | 2004-2009 | 17 | 200000 |
| Feit-Thompson theorem | 2006-2012 | 15 | 170000 |
| Flyspeck project | 2003-? | 16 | 325000 |
Table 1: Major verification efforts
The size and duration of these four big verification efforts is listed in Table 1. The verification of the four colour theorem is the earliest of and unique among the four projects in that the final proof has been created by a single person. The other three verifications are all team efforts with the size of the teams ranging between 15 and 17 people and considerably larger in terms of lines of code than the four colour theorem verification. Interestingly, the duration of all completed projects is roughly the same. This suggests that it is possible to tackle more complex verification problems within the same duration by dramatically increasing the number of people that are thrown at the verification effort.
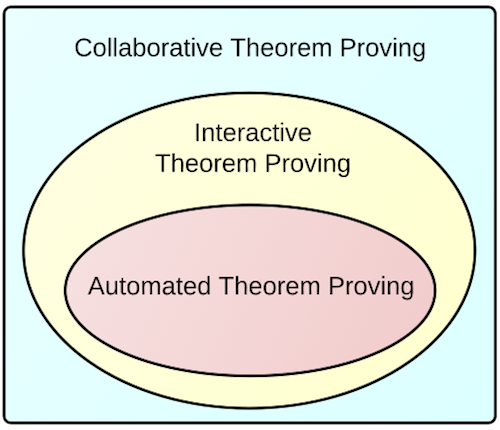
Figure 1
Interactive theorem proving can be understood as an extension of automated theorem proving by interaction between a single user and the prover software so that more complex problems can be attacked. We propose a further extension of interactive theorem proving by collaboration between many peers and the prover software: collaborative theorem proving (CTP). To indicate that the number of collaborators can be in the thousands, maybe even in the millions, we use the term massively collaborative theorem proving.
There are already flourishing examples of massive collaboration on the Internet to be found. Wikipedia is regularly used by about half of the Internet population, although the number of actual contributors is far less. StackOverflow is a Q&A site for programmers, with around 1.5 million users, and a total of 4 million questions and 7.5 million answers. Github is a site for hosting and sharing source code. It is based on the source code version control system Git and has around 2 million users hosting almost 4 million source code repositories. MathOverflow is a Q&A site for mathematicians, with around 17000 users and 30000 questions asked and answered. An interesting approach to solve open mathematical problems via Internet collaboration is put forward in the article Massively collaborative mathematics. The idea is to have some kind of online forum dedicated to solving a specific mathematical problem where anyone can contribute to the solution. The basic rule is to share a single idea per contribution, even if the idea is not fully developed yet. This approach was tested by the Polymath project: The specific aim was to find an elementary proof of a special case of the density Hales-Jewett theorem. The project was conducted on the blog of Timothy Gowers, attracting 27 contributors over a time span of 40 days. It was even more successful than originally anticipated in that the found elementary proof did not only prove the special case, but could also be generalised to a proof of the full density Hales-Jewett theorem. A question that this project leaves open though is if the Polymath approach can be scaled to considerably more than 27 contributors, especially using only such a simple organisational tool as a blog.
Inspired by the success of Wikipedia and daunted by the complexity of implementing an ITP system from scratch, so far all attempts at collaborative theorem proving take an existing ITP system and try to turn it into a CTP system by combining it with a web interface, either custom or based on existing Wiki software. This line of research is being pursued for example for Matita, Mizar, Coq and generically for any ITP system in principle.
We propose a more radical approach: Let’s take the challenge of CTP seriously and research how to design a CTP system from the ground up.
Design Objectives
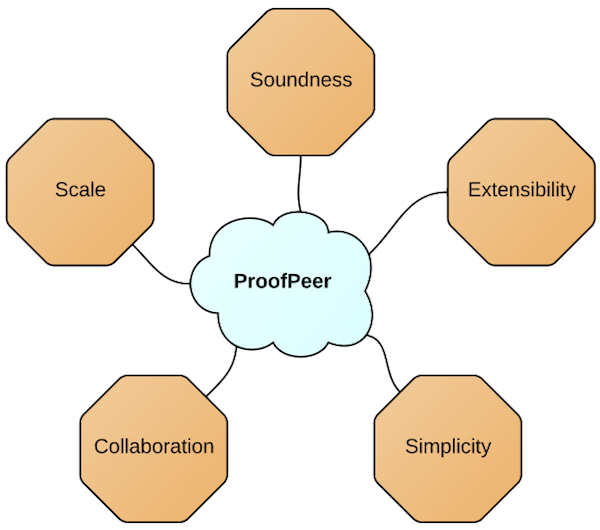
Figure 2
The design of ProofPeer is guided by placing equal importance on the design objectives illustrated in Figure 2. It is important to attack them simultaneously, e.g. collaboration should be simple but should also scale, should obviously not violate soundness, and it should be possible for third-party extensions of ProofPeer to be "collaboration-aware".
Scale
ProofPeer should be able to handle a very large number (i.e. several millions) of total users and a large number (i.e. tens of thousands) of concurrent users. These concurrent users will not just browse the content that ProofPeer offers, like it is the case with Wikipedia, but engage in potentially costly activities like doing proofs.
Soundness
ProofPeer is a theorem proving system. When ProofPeer states that something is a theorem then this statement must be reliable and it must be clear on what assumptions this statement rests.
Collaboration
There are two primary collaboration scenarios and many hybrid scenarios that combine these two, and ProofPeer should be catering to both of them. First, a team directly working together on a project like the Flyspeck project could use ProofPeer to host this project. Second, peers could work independently from each other but will nevertheless collaborate indirectly because they contribute to a shared common library of theorem proving artifacts. ProofPeer should be designed to establish a positive feedback loop between collaborative and theorem proving features.
Simplicity
Using ProofPeer should be as simple as possible but not simpler. Theorem proving is a challenging activity and some aspects of it might never be easy to understand for most people. That said, there are also many people that could learn theorem proving already at school age and it is important not to deter interested people from the beauty of the subject by unnecessary complexity.
Extensibility
Ever since Edinburgh LCF ITP systems have been fully programmable. This makes it possible to extend the system with custom tactics and custom automation. It also makes it possible to build domain specific applications on top of an ITP system. The challenge is thus to make a CTP system just as extensible as an ITP system without violating the other objectives of scale, soundness, collaboration and simplicity.
Architecture
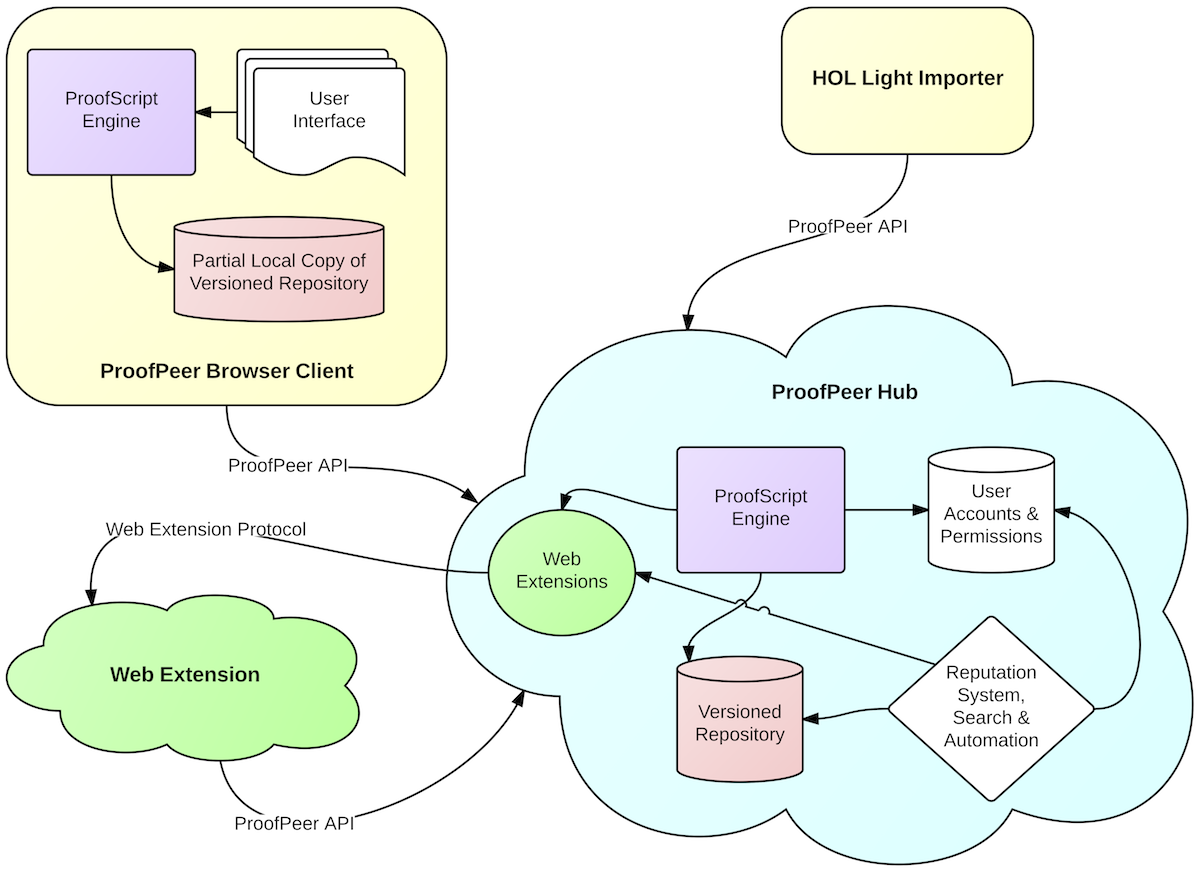
Figure 3
The high-level architecture of ProofPeer is depicted in Figure 3. We compose ProofPeer out of one central hub and any number of clients and web extensions. Clients connect to ProofPeer via an API based on JSON. Web extensions register with the hub via the same API and are called from the hub via the web extension protocol which is also based on JSON. Web extensions are ProofPeer's equivalent of a foreign function interface.
Technical Considerations
Because parts of both the ProofScript engine and the versioned repository need to be available both at client and at server side, we choose Clojure / ClojureScript as our main implementation language. This has the advantage that we can compile Clojure both to Java and to Javascript. We need Java on the server side where we use Google App Engine as our main cloud computing platform as Google App Engine has a high level of abstraction. We need Javascript on the client side because the client should run within any (modern) web browser like Google Chrome without any aditional installations. We are furthermore using on the client side the Google Closure tool suite together with Twitter Bootstrap and jQuery.
ProofScript
Our approach to achieve our design objectives for ProofPeer is language centric. We will define and implement a new language called ProofScript. ProofScript will be both a programming language and a proof language.
Figure 4: Hypothetical examples of ProofScript code
ProofScript will help us to achieve our ProofPeer design objectives.
- ProofScript will support scale because it is a purely functional programming language. This means that values that have been computed once can be cached and reused by many peers at the same time.
- ProofScript is essential in guaranteeing the soundness of derived theorems. There will be a type of theorems and the only primitive operations allowed to create and manipulate theorems are those defined by the underlying logic. Note though that ProofScript could be dynamically typed.
- All proof scripts must live in namespaces. This is a necessary prerequisite for collaboration. Furthermore, the collaboration oriented components of ProofPeer like versioning, continuous integration, search and even the reputation system will be codesigned with ProofScript.
- ProofScript also serves our quest for simplicity. Because it is both a programming language (partially inspired by Babel-17) and a proof language (heavily inspired by Isabelle/Isar) users only need to learn a single language instead of at least two (and worse, also how these two interact) like in most popular ITP systems.
- ProofScript will be the most direct way to extend ProofPeer. Because ProofScript is a programming language, new tactics and decision procedures can be coded up in a safe way on top of existing ones.
Which Logic?
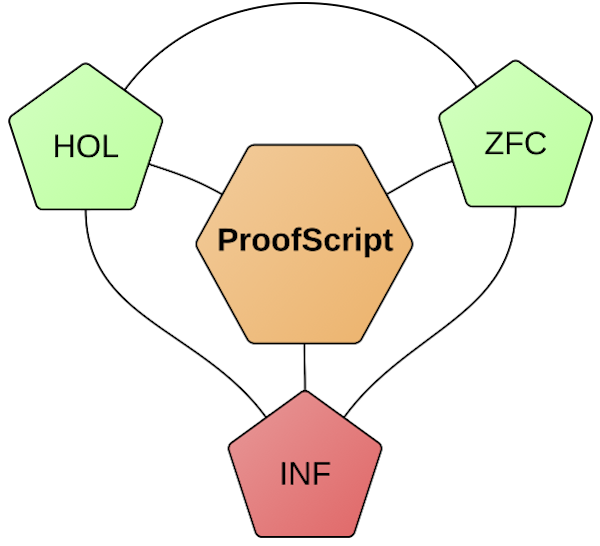
Figure 5
It is intuitively clear that much of ProofPeer does not depend on a particular logical system. We will nevertheless focus on a particular logic. This has two main advantages: 1) we can integrate ProofScript tighter with the logic, 2) there is less of a risk for the ProofPeer community to become fragmented.
Furthermore, experience has shown that even when the system is designed as a logical framework like Isabelle, the majority of users will focus on a particular logic of that system (Isabelle/HOL) anyway.
Although we have not decided yet on the particular form of the logic we are going to use, we already know important properties we want it to have:
- it must contain simply-typed higher-order logic (HOL), which is well suited for formalising functional programs and actually executing them,
- in particular, it must be compatible with HOL Light, which we will use to bootstrap ProofPeer,
- it should contain Zermelo-Fraenkel set theory (ZFC), which is more familiar to mathematicians and admits constructions not possible in HOL, like Scott’s inverse limit construction,
- it should provide transfer principles between HOL and ZFC.
Informal reasoning
The Polymath project shows how important informal collaboration on the Internet could become in mathematical practice. Furthermore, many formal proof developments start out with an informal proof. That is why it is important to have support for informal reasoning (INF in Figure 5) as part of ProofScript. Of course, for the sake of soundness we must keep track of those theorems that have been proven with the help of informal reasoning and warn the user that these theorems are not formally proven. The support for informal reasoning generalizes constructs like "sorry" in Isabelle/Isar and makes proof sketches possible.
Conjectures
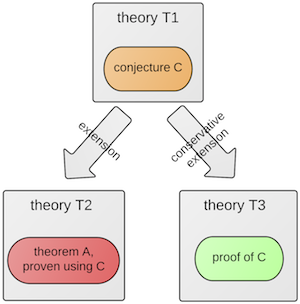
Figure 6
We would like to make it possible to conjecture theorems in ProofPeer. Conjectures have been recognized as an interesting topic in interactive theorem proving previously. In ProofPeer, conjectures could be a powerful tool for organising and distributing formalisation work among peers. Here is how we would like conjectures to work in ProofPeer:
- A conjecture C is declared in some theory T1.
- It is now possible to use C as a theorem in theories (say in theory T2) that extend from T1. The theorems that are proven in T2 with the help of C will be marked as being dependent on the validity of C. In Figure 6 this is exemplified by theorem A.
- It is also possible to prove C in theories (say in theory T3) that conservatively extend T1. This proof must not depend on C. If C thus is proven in T3, it can be used as a valid theorem in all theories that extend T1, in particular also in T2!
Web Extensions

Figure 7
Although ProofScript is a powerful language there will always be situations when non-ProofScript programs need to be used as part of the formalisation effort. Typically these programs are already existing third-party software that is used to quickly compute certificates which are then turned into fully formal proofs. Examples of this approach are obtaining upper bound certificates for linear programs via the dual linear program by calling GLPK from Isabelle, or reconstructing Z3's bit-vector proofs in HOL4 and Isabelle/HOL.
Because ProofPeer runs in the cloud the question arises how it can be extended to call third-party software like GLPK or Z3. We propose the mechanism of web extensions for this. Web extensions relate to ProofScript in about the same way that other foreign function interfaces relate to languages like Lisp or Haskell. A web extension is running somewhere on the Internet, usually outside of the ProofPeer cloud, and can be called from ProofPeer via the web extension protocol. Figure 7 shows how a web extension for computing upper bound certificates for linear programs could be registered with ProofPeer.
How is it ensured that web extensions do not impact the soundness of ProofPeer? This is very simple indeed: we just require that the result returned by calling a web extension must not contain a value of type theorem.
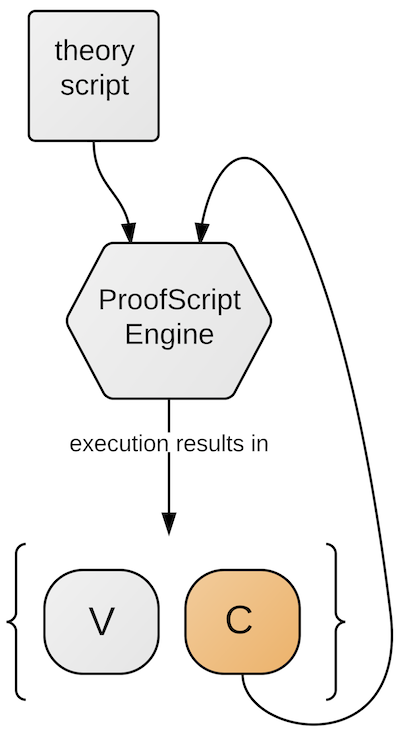
Figure 8
A problem with web extensions is that ProofPeer has no control over the availability and semantics of the web extension. For example, the GLPK web extension might have vanished from the Internet without notice, or it might have changed because a new version of GLPK has been installed on the server which provides the GLPK web extension. The reason this is problematic is that ProofPeer is supposed to guarantee that once a theory has been accepted by the system it can be replayed at any later point in time. But the web extension might not be available anymore at that later point in time! A possible solution to this dilemma is to make all web extensions by default cached.
Cached Functions
The result of executing a ProofScript theory/program is a mapping V from identifiers to computed values. For example, executing the theory in Figure 7 leads to a mapping from the identifier dual_glpk to some function, and from the identifier certificate to some two-dimensional vector. The idea is that by declaring a function as cached, this result is augmented by a mapping C that records (possibly a subset of) all input/output pairs that have been computed for this function during the execution of the script. The next time the script is executed, C could be passed to the execution engine along with the script to be executed, and when the engine encounters a function call that is covered by C, instead of executing the function call the engine just looks up the respective value in C (Figure 8).
This mechanism could also be useful to shift load from the ProofPeer hub to the clients that connect to ProofPeer. When a client executes a proof script locally, it will also compute C along with V. When then the client submits the script to the hub, it can also pass C to the hub. The server can then avoid costly recomputation of those function calls already covered by C. There is one exception to this: C may not contain values that contain theorems.
HOL Light Import
We will provide an import facility from HOL Light to ProofPeer in order to quickly get valuable initial content into ProofPeer and to turn it into a useful system. We will go beyond previous work that imported HOL Light theorems via proof objects into Isabelle by also automatically porting tactics like MESON_TAC. Our hopes for this task are that we will be able to import those parts of the Flyspeck project into ProofPeer which have been carried out in HOL Light.
Versioning & Continuous Integration
The ProofPeer library will consist of a set of theories, where each theory is a proof script. Each theory has a unique name which is also used as a namespace for the proof script.
Theories depend on each other and are concurrently modified by many peers. Without versioning this would result in chaos, as each peer would find herself in an ever changing environment that invalidates a proof script as soon as it is written down. Versioning each theory separately is no real help either, as the dependencies between theories would be lost. Modern distributed source code version control systems like Git provide the needed inspiration: Versioning does not happen on the basis of single theories, but on the entire content of the repository! This means that modifying a single theory creates a whole new snapshot of everything. A series of changes thus results in a series of snapshots called a branch (Figure 9).
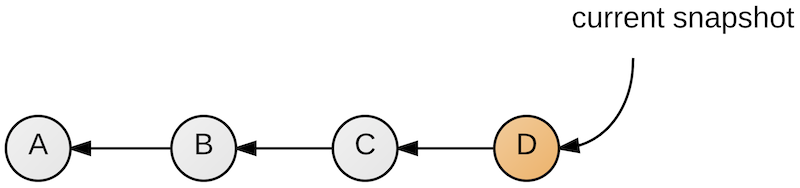
Figure 9: A branch consisting of snapshots A, B, C and D
The crucial idea we are proposing is to treat the entire library of ProofPeer as a single repository. There will be a public branch which acts as the official history of the ProofPeer library. Each time a peer starts modifying the library, she will do so on a separate branch. This ensures two things: First, she is shielded during her work from any changes that are made to the library by others; second, everyone else is shielded from her changes (Figure 10)!
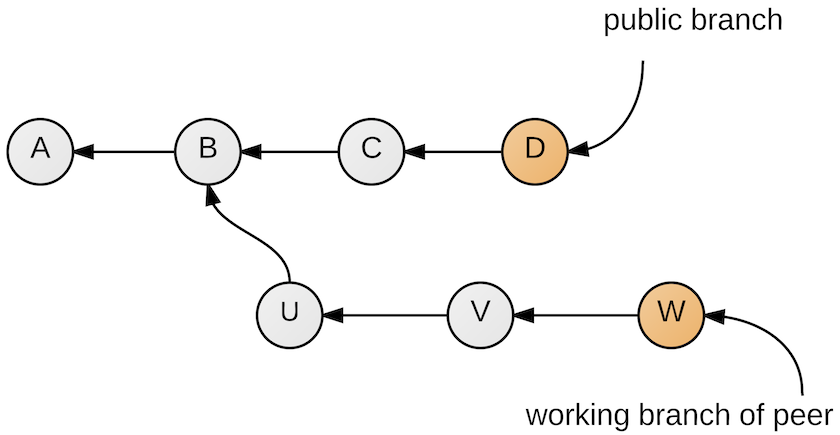
Figure 10
Of course, eventually she will want to see changes made by others; this can be achieved by merging the public branch into her own branch (Figure 11).
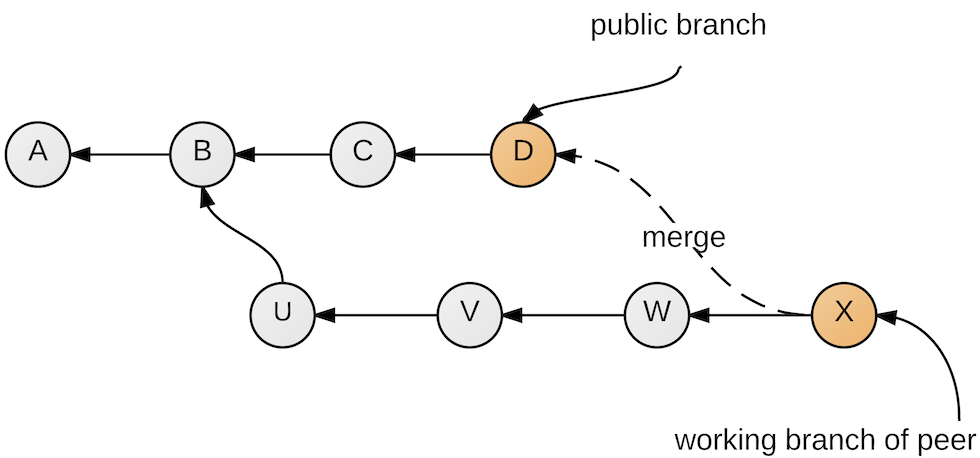
Figure 11: Pulling from the public branch
On the other hand, if she wants to make available her work to others, then her branch will be merged into the public branch (Figure 12).
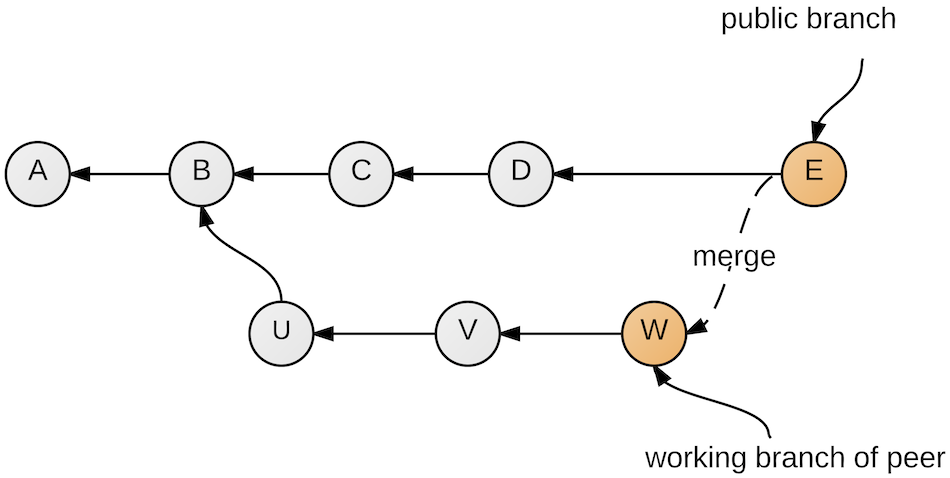
Figure 12: Pushing to the public branch
Theories are just text files, so we can use well-established algorithms for merging text; but because we know the structure of theory files, we intend to come up with an even better merge algorithm especially designed for theory files.
Privacy & Permissions
Although our ultimate goal is collaboration, we also need to provide for the fact that not every theory is supposed to be seen by everyone else, at least not until it has reached a certain publishable state. Similarly, not every theory is supposed to be modifiable by everyone else. It is tempting to treat both kinds of permissions, viewing a theory, and modifying a theory, in a similar generic way, e.g. by having a permission matrix assigning to each combination of theory and peer the set of permissions that the peer has with regard to the theory. Nevertheless, the two permissions are of a very different nature, as the following thought experiment shows: Imagine theory B consists of theorems about notions defined in theory A, and both theories are publicly visible and publicly modifiable. Now, theory A is changed to be only privately visible. But theory B is still publicly visible! So a peer will find herself in the unfortunate situation to be able to read theory B, but to not fully understand it, because for a full understanding she would also need access to theory A which defines the notions that B talks about. Changing instead the modify-permission of theory A, though, has no such negative transitive effect.
This suggests the following solution:
- Modify-permissions of theories are dealt with in a traditional way via a permission matrix.
- Read-permissions are managed by granting read-access to entire branches. In this way if a user can read a theory then she can also read all theories in the same snapshot!
Dependency Tracking and Continuous Integration
Because a theory is just a ProofScript program, checking it means executing it. The result of a check that succeeded will be a mapping from identifiers to computed values which is stored together with the respective snapshot so that every theory in a given snapshot is checked at most once. Changing a theory means that all directly or indirectly depending theories need to be rechecked as well. By not only keeping track which theories depend on each other, but also which named values in theory A a given named value in theory B depends on, it is likely that the process of rechecking can be optimised further.
Not only theories may change, but also the ProofScript language and logic itself. This can be taken into account by introducing a special root theory which every other theory depends on and make the root theory part of the versioned repository, too. A change of ProofScript itself now corresponds to a change of the root theory.
Reputation System, Search & Automation
This is the prize we are really after. Let us assume for a moment that millions of peers are already using ProofPeer. This would yield a huge library of formalisations; and an immense amount of usage data about what peers are proving and how they are proving it. How do we curate this huge library? How do peers search the library to find theorems and techniques they can use for their own formalisations? And, can we feed the usage data into machine learning algorithms to improve theorem proving automation?
Reputation System
Traditionally, formal libraries of ITP systems like the Mizar library, the Archive of Formal Proofs, or the Mathematical Components Project are manually curated by a fixed small team of experts. This approach breaks down when facing a library created by millions of peers, but we can still try to capture the essence of this idea: Some peers will be better at using ProofPeer than others. These should form the group of experts in charge of library curation. To identify this group of experts we will establish a reputation system that scores peers and their formalisations. The higher the score of a peer the more power this peer can wield within ProofPeer.
A lot of research and experimentation will be needed to come up with a good reputation system. A common mechanism employed by sites like StackOverflow or Hacker News is to allow votes on user contributions and then to determine the reputation score of a user as the sum of the votes of all of the user's contributions. To apply this to ProofPeer we first have to determine what the contributions of a peer are. Obviously theories are contributions, but theories can be authored by multiple peers. It also seems reasonable to allow voting on a more granular level than theories, like theorems and definitions. The issue is further complicated by the fact that the library evolves in time, theories change, and ownership changes. As an example, assume a popular theorem breaks (i.e. its proof does not check anymore) because a constant occurring in it has been replaced by an equivalent but differently defined constant. A curator (who did not originally author the theorem and its proof) rushes in and fixes the theorem and its proof by restating it in terms of the new constant. Now, do we want to transfer the votes from the old theorem to the new theorem? If yes, how do we determine that the new theorem is just an updated version of the old theorem? And how much credit should the curator get as she basically just contributed a minor fix of the theorem, not the theorem itself?
In addition to direct user votes theorems and definitions could also be scored according to their usage. The more a theorem or a definition gets used in proofs by other peers the higher its assumed value would be. This suggests calculating the score of theorems and definitions in a fashion similar to Google's page rank algorithm. There is an obvious problem with this: A counter example where this calculation would fail would be the scoring of Fermat's Last Theorem, which is certainly an impressive result deserving a high score, but which does not have many applications in other proofs. A possible solution could be to take user votes as a rank source for the page rank algorithm, combining the two methods of direct voting and voting via usage. Another solution could be just not to combine them and just keep separate scores.
Search & Automation
A straightforward way to approach search in a mathematical library is pattern-based: Given a search pattern, look up the corresponding matches in the library, possibly taking into account sub patterns etc. This approach is for example pursued with Whelp, MathWebSearch and MIaS.
An immediate way to improve pattern-based search could be to weigh the search results according to the score that is associated with them via the reputation system.
Pattern-based search asks the system the question "search for something that looks LIKE THIS" where LIKE THIS is specified by the pattern. Another, very promising approach to search is characterised by the question "search for something that can help me WITH THIS" where WITH THIS describes the current context you are in. This context could for example be that you are currently trying to prove a certain theorem. If we are able to characterise the context numerically then we can try to apply machine learning techniques for finding the things that are helpful in a certain context.
A spectacular result in that direction is claimed by Kaliszyk and Urban. They have applied premise selection methods based on machine-learning to the Flyspeck formalisation code base and used them to prove almost 40% of the Flyspeck theorems automatically with automated provers like E, Z3 and Vampire. The problem with applying automated theorem provers to interactive theorem proving is that their applicability rapidly shrinks with the number of premises they have to consider. Premise selection methods are therefore used to filter out relevant premises for the theorem under consideration out of the existing library of theorems. In this way premise selection forms a remarkable bridge between search and automation.
The machine learning methods used by Kaliszyk and Urban use the theorems themselves and the information on what other theorems the proofs of theorems depend. Another interesting approach is to look directly at the proof of a theorem, in particular its structure, and try to learn properties of proofs. This approach is pursued by Komendantskaya who is using neural networks to learn proof-patterns. It is worthwile to examine how to combine such learning with our reputation system: Could we for example learn to distinguish between beautiful proofs and ugly proofs automatically by learning proofs based on their score?
We will start our exploration of this area by implementing web extensions that access automated provers, in particular Z3. Previous work has shown how to integrate Z3 in a safe way with ITP systems, and we will build on that work. From there we will explore how to improve search and automation by combining our reputation system with the machine learning methods mentioned above.
User Interface
Proof General is the most popular user interface for ITP systems. An alternative interaction model is the PIDE approach. This approach is utilized by the Clide system, which will serve us as a starting point.
An improvement over current user interfaces we will examine is how to better visualise tactic style proofs. A promising framework for such a visualisation is the notion of hiproofs.
Besides a user interface for interactively editing proof scripts we must also provide adequate user interface abstractions for dealing with other features of ProofPeer like versioning.
Example of a Hiproof Visualisation
(this example will work properly only in recent browser versions that support HTML 5)
This is an example from our research into how to visualise HOL Light proofs via hiproofs. Below you see the
HOL Light source code for the prove of the lemma TRANSITIVE_STEPWISE_LT_EQ:
let TRANSITIVE_STEPWISE_LT_EQ = prove
(`!R. (!x y z. R x y /\ R y z ==> R x z)
==> ((!m n. m < n ==> R m n) <=> (!n. R n (SUC n)))`,
REPEAT STRIP_TAC THEN EQ_TAC THEN ASM_SIMP_TAC[LT] THEN
DISCH_TAC THEN SIMP_TAC[LT_EXISTS; LEFT_IMP_EXISTS_THM] THEN
GEN_TAC THEN ONCE_REWRITE_TAC[SWAP_FORALL_THM] THEN
REWRITE_TAC[LEFT_FORALL_IMP_THM; EXISTS_REFL; ADD_CLAUSES] THEN
INDUCT_TAC THEN REWRITE_TAC[ADD_CLAUSES] THEN ASM_MESON_TAC[]);;
Exporting this through our visualisation tool and manually adding some hierarchy yields the graph below. Note that you can see intermediate goals by hovering over edges, and make these goals permanently visible by clicking on them.